Résolution de systèmes linéaires

Dans cet ED, nous allons nous intéresser à une méthode de résolution directe de systèmes linéaires : la méthode de résolution de Gauss et décomposition « LU ».

Vous avez 3h40min pour réaliser le TP (8h00-11h40 ou 13h30-17h10). À l’issue de ce temps, vous présenterez un bilan de vos travaux et de vos résultats pendant 10 min maximum. S’en suivront 10 min de questions. L’ensemble sera évalué par une note attribuée à la totalité du groupe. La totalité des supports présentés seront exclusivement manuscrits (pas de diaporama ni d’impressions informatiques) au format A5 paysage.
Critères d’évaluation : fond (rigueur scientifique, résultats, etc.), forme (supports, prestation, etc.) et analyse (problématique, plan, etc.).

TABLE DES MATIÈRES

Introduction

L’ensemble de ce sujet est écrit pour être appliqué au logiciel Microsoft Excel.

Système d’ordre 3

Dans cette partie, une feuille de calcul va être réalisée pour pouvoir résoudre l’équation suivante :

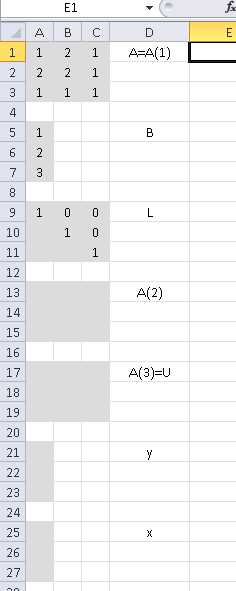
$\left\lbrace \begin{array}{l@{~=~}l} x+2y+z&1 \\ 2x+2y+z&2 \\ x + y + z &3 \end{array}\right.$

Pour cela, il faut commencer par construire une feuille Excel qui pourrait ressembler à la capture suivante :

La méthode est détaillée dans le cours. Rappelons les principales étapes :

déterminer les matrices $L$ et $U$ tels que $A=LU$
déterminer la matrice $y$ telle que $Ly=B$
déterminer la matrice solution $x$ telle que $Ux=y$

Construction des matrices $L$ et $U$

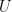
L’algorithme de Gauss consiste à poser $A^{(1)}=A$ et à calculer pour $k=1,2,\dots ,n$

$l_{ik}=\dfrac{a_{ik}^{(k)}}{a_{kk}^{(k)}} ~~~~~ i=k+1,k+2, \dots ,n$

$a_{ij}^{(k+1)}=a_{ij}^{(k)}-l_{ik}a_{kj}^{(k)} ~~~~~ i=k+1, k+2, \dots , n$

À la fin de ce procédé, les éléments de la matrice $U$ sont définis par :

$u_{ij}=a_{ij}^{(i)}$

Pour notre exemple d’application, nous avons :

$A=\left[ \begin{array}{ccc} 1&2&1 \\ 2&2&1 \\ 1&1&1 \end{array}\right]$ et $B=\left[ \begin{array}{c} 1 \\ 2 \\ 3 \end{array}\right]$

Pour $k=1$ , $i=2$ et $i=3$

Pour $i=2$

$l_{21}=\dfrac{a_{21}^{(1)}}{a_{11}^{(1)}}$ ce qui donne A10=A2/A1=2

Pour $i=3$

$l_{31}=\dfrac{a_{31}^{(1)}}{a_{11}^{(1)}}$ ce qui donne A11=A3/A1=1

NB. Il aurait également été possible de définir A10=A2/$A$1 et de faire glisser à la cellule d’en dessous ce qui nous aurait donné A11=A3/$A$1

La première colonne de $L$ est terminée. Passons à la construction de $A^{(2)}$ . Nous commençons à la ligne $i=2$ donc la première ligne de $A^{(2)}$ est identique à celle de $A^{(1)}=A$ .

Pour $i=2$

Pour $j=1$

$a_{21}^{(2)}=a_{21}^{(1)}-l_{21}~a_{11}^{(1)}$ soit A14=A2-A10*A1=0

Pour $j=2$

$a_{22}^{(2)}=a_{22}^{(1)}-l_{21}~a_{12}^{(1)}$ soit B14=B2-A10*B1=-2

Pour $j=3$

$a_{23}^{(2)}=a_{23}^{(1)}-l_{21}~a_{13}^{(1)}$ soit C14=C2-A10*C1=-1

Pour $i=3$

Pour $j=1$

$a_{31}^{(2)}=a_{31}^{(1)}-l_{31}~a_{11}^{(1)}$ soit A15=A3-$A$11*A1=0

En faisant glisser sur la droite, B15=-1 et C15=0

Au final $A^{(2)}=\left[ \begin{array}{ccc} 1&2&1 \\ 0&-2&-1 \\ 0&-1&0 \end{array}\right]$

Q1. Réaliser la suite du calcul pour le(s) $k$ suivants et vérifier que vous avez les bonnes matrices $L$ et $A^{(3)}$ grâce à votre cours.

Construction de la matrice 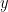$y$

$L$ est une matrice triangulaire inférieure. Nous cherchons $y$ tel que $Ly=b$

$\left\lbrace \begin{array}{ll} y_1=\dfrac{b_1}{l_{11}}& \\y_i=\dfrac{1}{l_{ii}} \left[ b_i-\displaystyle \sum_{j=1}^{i-1} l_{ij}y_j\right]&i=2,3,\dots ,n \end{array}\right.$

$y_1=\dfrac{b_1}{l_{11}}$ équivaut à A21=A5A9=1

Pour $i=2$ (et nous terminerons par $i=3$ )

$y_2=\dfrac{1}{l_{22}}~\left[ b_2-\left( l_{21}~y_1 \right) \right]$ soit A22=1/B10*(A6-A10*A21)=0

Q2. Terminer la matrice $y$ .

Construction de la matrice $x$

$U$ est une est une matrice triangulaire supérieure. Nous cherchons $x$ tel que $Ux=y$

$\left\lbrace \begin{array}{ll} x_n=\dfrac{y_n}{u_{nn}}&\\x_i=\dfrac{1}{u_{ii}} \left[ y_i-\displaystyle \sum_{j=i+1}^{n} u_{ij}x_j \right]& i=n-1,n-2,\dots ,2,1\end{array}\right.$

$x_3=\dfrac{y_3}{u_{33}}$ équivaut à A27=A23/C19=4

Pour $i=2$ (et nous terminerons par $i=1$ )

$x_2=\dfrac{1}{u_{22}} \left[ y_2-\left( u_{23}~x_3 \right) \right]$ soit A26=1/B18*(A22-(C18*A27))=-2

Q3. Terminer la matrice $x$ .

Système d’ordre 6

Q4. Programmer une feuille de calcul pour pouvoir résoudre l’équation suivante :

$\left\lbrace \begin{array}{l@{~=~}l} 2x+3y+z+2u-3v+3w&2\\2x+2y+z+2u+3v+4w&4\\-x+y+z-2u+4v-w&1\\2x+3y-z+u+2v+w&-2\\x+2y-3z+u+v+2w&4\\4x+y-2z+4u+2v+w&1\end{array}\right.$

Ou encore, appliquer la méthode précédente avec :

$A^{(1)}=\left[ \begin{array}{cccccc}2&3&1&2&-3&3\\2&2&1&2&3&4\\-1&1&1&-2&4&-1\\2&3&-1&1&2&1\\1&2&-3&1&1&2\\4&1&-2&4&2&1\end{array}\right]$

et $B=\left[ \begin{array}{c}2\\4\\1\\-2\\4\\1\end{array}\right]$

Quelques indices pour vous aider dans les étapes de calcul:

$A^{(2)}=\left[ \begin{array}{cccccc}2&3&1&2&-3&3\\0&-1&0&0&6&1\\0&2.5&1.5&-1&2.5&0.5\\0&0&-2&-1&5&-2\\0&0.5&-3.5&0&2.5&0.5\\0&-5&-4&0&8&-5\end{array}\right]$

$A^{(3)}=\left[ \begin{array}{cccccc}2&3&1&2&-3&3\\0&-1&0&0&6&1\\0&0&1.5&-1&?&?\\0&0&-2&-1&5&-2\\0&0&-3.5&?&?&?\\?&?&-4&0&?&?\end{array}\right]$

$A^{(4)}=\left[ \begin{array}{cccccc}2&3&1&2&-3&3\\0&-1&0&0&6&1\\0&0&1.5&-1&?&?\\0&0&0&?&?&?\\0&0&0&?&?&?\\0&0&0&?&?&?\end{array}\right]$

$A^{(5)}=\left[ \begin{array}{cccccc}2&3&1&2&-3&3\\0&-1&0&0&6&1\\0&0&1.5&-1&?&?\\0&0&0&?&?&?\\0&0&0&0&18&6\\0&0&0&0&?&?\end{array}\right]$

$A^{(6)}=\left[ \begin{array}{cccccc}2&3&1&2&-3&3\\0&-1&0&0&6&1\\0&0&1.5&-1&?&?\\0&0&0&?&?&?\\0&0&0&0&18&6\\0&0&0&0&0&-1.7142\end{array}\right]$

$y=\left[ \begin{array}{c}2\\2\\7\\?\\?\\6\end{array}\right]$

$x=\left[ \begin{array}{c}-20\\?\\?\\19\\2\\-3.5\end{array}\right]$

Q5. Donner le résultat de cette méthode appliquées à la matrice suivante :

$A^{(1)}=\left[ \begin{array}{cccccc}1&2&1&0&0&0\\2&2&1&0&0&0\\1&1&1&0&0&0\\0&0&0&1&0&0\\0&0&0&0&1&0\\0&0&0&0&0&1\end{array}\right]$

et $B=\left[ \begin{array}{c}1\\2\\3\\0\\0\\0\end{array}\right]$

Q6. Résoudre le système d’équation à 5 inconnues suivant :

$\left\lbrace \begin{array}{l@{~=~}l} 2x - 3y + z&5 \\ -3x + y + 2u&5 \\ 5y - 2z + 3t&6 \\4z - 5t + u&6 \\ -4x + 2t - 3u&-17 \end{array}\right. %Les réponses sont x = 2, y = 1, z = 4, t = 3 et u = 5$